rubus0304 님의 블로그
[통계 라이브세션2] 주요 강의내용 정리 본문
내용: 가설설정, 통계적 유의성, 가설검정 - 이론
99% 신뢰구간이 더 넓어져서 모수를 추측하기 어려워서 좋다 나쁘다 고를 수 없음. 95% 신뢰구간이 더 신뢰가 높음!
이번 강의에서 배울 것
- 변수: 대상의 속성이나 특성을 측정하여 기록한 것
- 독립변수: 원인이 되는 변수로, 설명변수라고도 불립니다.
- 종속변수: 결과가 되는 변수로, 결과변수라고도 불립니다. 독립변수에 따라 그 값이 변할 것이라고 예상하는 변수입니다.
- 모수: 모집단을 대표하는 값
- 모수통계: 모집단이 정규분포를 따른다는 가정하에 사용됩니다. 데이터분석가는 주로 모수통계를 진행하게 됩니다. ****평균, 분산 등의 값을 알고 있다는 가정 하에 진행하는 통계분석이 되겠습니다.
- 비모수통계: 모집단이 정규분포가 아닐 때 사용됩니다. (이 말은 곧 표본의 크기가 충분히 크지 않음: 소규모 실험에 해당). 또는 평균, 분산 등의 값을 가정하지 않고 진행하는 통계분석입니다.

chi-square - 카이제곱
이번시간에는 A/B 테스트 라는 분석기법에 필요한 아래 3가지 통계적 지식을 학습하겠습니다.
- 가설설정
- 통계적 의미 해석(P-value)
- 가설검정(T검정, 카이제곱검정)
통계적 실험

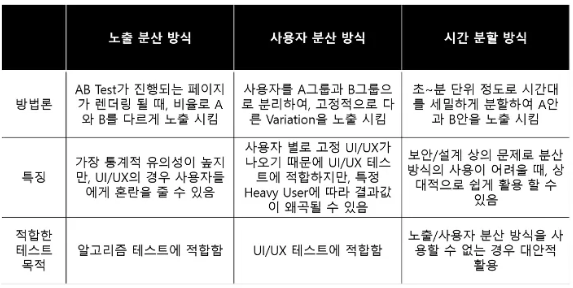
A/B 테스트


- A/B 테스트 주의사항
- 적절한 표본 크기: 표본의 크기가 충분하지 않으면 유의미한 결과를 얻을 수 없습니다. 적절한 표본 크기를 결정하고, 그에 맞는 시간과 자원을 투자해야 합니다.
- 하나의 변수만 변경: A/B 테스트에서는 하나의 변수만을 변경해야 합니다. 두 가지 이상의 변수를 동시에 변경하면 어떤 변수가 영향을 미쳤는지 파악할 수 없습니다.
- 무작위성: A/B 테스트는 무작위로 선택된 사용자들에게 각각 다른 변수를 적용해야 합니다.
- 적절한 분석 방법: A/B 테스트 결과를 해석할 때는 가설 검증을 위한 통계적 분석 방법을 선택하고, 유의수준을 설정해야 합니다.
- 테스트 결과의 의미: A/B 테스트 결과가 통계적으로 유의미하더라도 항상 실제로 의미 있는 결과인지 한번 더 생각해보아야 합니다.
- 정해진 기간 동안 진행: A/B 테스트는 동일한 기간 동안 진행되어야 합니다. 그 기간 동안에만 결과를 수집하고, 분석해야 합니다. 너무 짧은 기간 동안에는 결과를 수집하기 어렵고, 너무 긴 기간 동안에는 사용자들의 행동이 변할 가능성이 있습니다.
유의수준 설정하기
신뢰수준의 반대 개념
중심극한정리 복습
중심극한정리는 표본수집을 기반으로 한 추리통계에서 모집단의 분포가 어떤 모양이더라도 모집단의 크기가 충분히 크다면 표본평균의 분포가 정규분포를 이룬다는 이론이였습니다. 그리고 이를 통해, 모집단의 모수를 추정할 수 있습니다.
유의수준
지난 시간에서 학습했듯이, 표본을 추출하는 순간 모집단과 100% 일치할 수 없기 때문에, 오류의
가능성이 존재한다고 학습했습니다. 가설 검정에서 결론을 해석하기 위해서는 기준을 세우고,
그 기준을 만족하는지 확인해야 합니다. 여기서 기준이 되는 것이 유의수준입니다
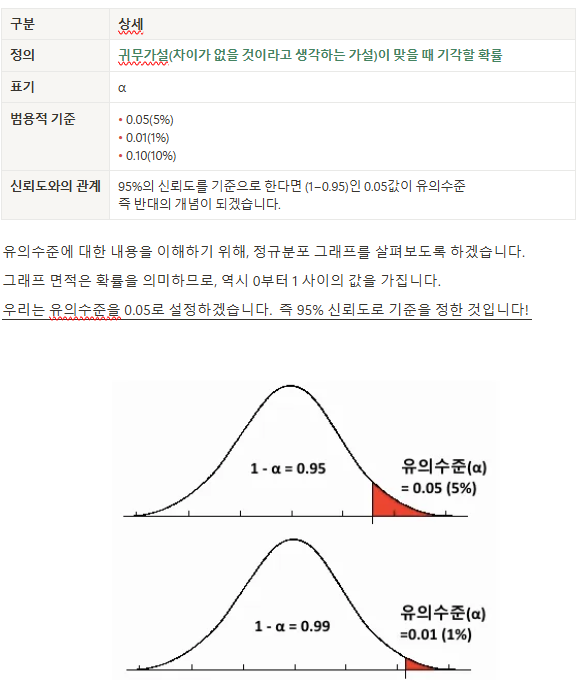
보통을 유의수준을 지정하면 자동으로 신뢰구간이 지정. 예를 들어 유의수준 0.05 지정하면 자동으로 신뢰구간이 0.95로 지정됨..
검정통계량과 p-value
유의수준을 정하고 실험을 진행했어요. 결과를 해석하고 싶어요!
- 결과 해석 단계 1: 검정 방식 정하기 & 검정통계량 계산하기실험을 완료한 뒤, 실험 전과 후를 비교하면서 유의미했는지 살펴봐야겠죠!
- 검정통계량이란 귀무가설을 채택 또는 기각하기 위해 사용하는 확률변수를 의미합니다.→ 즉 확률에 대한 수치이므로, 0과 1 사이의 값을 가지게 됩니다.
- → 확률변수란, 특정 확률로 발생하는 각각의 결과를 수치값으로 표현하는 변수입니다. 📙
- 결론적으로 우리는 귀무가설을 채택할지, 기각할지 결정할 수 있어야 합니다.
- 우리는 지금까지 가설을 설정하고 유의수준을 정했습니다.

함수 지정하면 자동으로 검정통계량이 계산되서 나옴.
검정통계량은 표본 평균, 비율, 상관 계수 간의 차이 등 다양한 형태를 취할 수 있습니다. 검정방
식의 선택은 가설과 데이터 종류에 따라 달라집니다. 아래 표에서 확인해 보겠습니다.
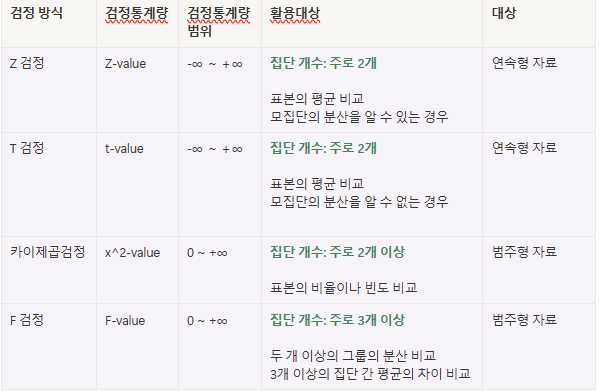
이런 값을 갖고 있구나 보고 판단은 P-value 로 함.
실습은 T검정, 카이제곱검정으로 할 거임.
(차이) z- 검정: 모집단의 분산을 알 수 있는 경우/ T검정: 모집단의 분산을 알 수 없는 경우
- 카이제곱은 제곱 써서 무한대 없고 0부터!
- F-value 주로 집단 3개 이상. 두 개 이상의 그룹 분산 비교, 3 개 이상의 평균의 차이 (=ANOVA) 많이 할 일은 없음.
결과 해석 단계 2: p-value
p-value: 어떠 사건이 우연히 발생할 확률
p-value 는 Probability-value 의 줄임말로 ‘확률’을 뜻합니다.
확률이므로, p-value 는 0 이상이고 1 이하의 값을 가지게 됩니다.
우리의 목표는 대립가설 채택이므로, 우연히 일어날 확률이 작으면 좋겠죠?
즉 유의수준보다 p-value 가 작은 경우에 우연히 일어날 가능성이 거의 없어 대립가설을 채택하
게 될 수 있습니다.
*귀무가설이 내가 주장하는 대립가설의 반대.

이를 그래프로 함께 살펴보도록 하겠습니다.
지난 시간에 학습했던 중심극한정리를 통해, 모집단이 큰 경우 표본평균이 정규분포를 따르게 된
다고 가정하도록 하겠습니다. p-value 는 정규분포 그래프에서 아래와 같이 확인할 수 있습니다.
정규분포의 그래프 아래쪽이 확률값이라는 사실을 기억해주세요! 🙂
우리는 유의 수준을 설정하고, p-value 를 도출해서 의미를 해석한다는 점 역시 잊지 말아주세요!
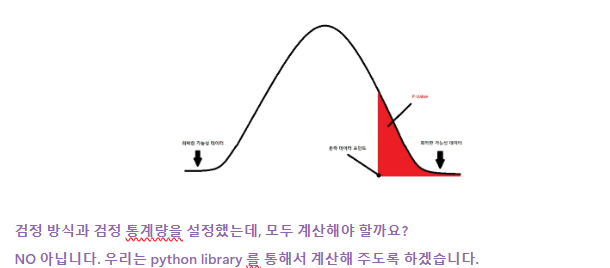
저 빨간 부분이 P-Value
금일 수업 요약
- 데이터분석가는 데이터 종류에 따라 알맞은 분석기법을 활용해야 합니다.
- A/B 테스트라는 방법론을 통해 해당 과정에서 사용되는 통계개념을 학습했습니다.
- 이는 가설설정, 통계적 의미 해석, 가설검정이 되겠습니다.
- A/B 테스트는 5가지 단계로 진행됩니다.
- 현행데이터탐색 → 가설설정 → 유의수준설정 → 실험 → 해석
- 귀무가설과 대립가설의 의미는 아래와 같습니다.
- 귀무가설은 차이가 없거나 의미 있는 차이가 없는 경우의 가설입니다.
- 대립가설은 차이가 있는 경우의 가설입니다.
- 유의수준은 신뢰도의 반대 개념입니다.
- 오류의 허용 범위=일반적으로 0.05를 사용합니다.
- 이는 곧 신뢰도 95% 를 의미합니다.
- p-value 는 어떠한 사건이 우연하게 발생할 확률입니다.
- p-value가 0.05 보다 작다 = 우연히 일어났을 가능성이 거의 없다 = 인과관계가 있다고 추정 = 대립가설 채택
- 우리는 python library 를 통해서 가설검정을 진행해 보았습니다.
'Data Analyst > 라이브세션' 카테고리의 다른 글
| [통계야 놀자 4회차] 회귀분석 (1) | 2024.11.19 |
|---|---|
| [통계야 놀자 3회차] 복습 & 실습 (1) | 2024.11.18 |
| [라이브세션 6주차] 강의정리 (0) | 2024.10.31 |
| [라이브러리 세션] 실습 (0) | 2024.10.30 |
| [라이브세션 과제] 판다스 라이브러리 (10/28, 10/29, 10/30, 10/31) (0) | 2024.10.28 |


