[통계학] 통계야 놀자 - 3회차
[통계학] 통계야 놀자 - 3회차 | Notion
[강의자료 PDF]
teamsparta.notion.site
ROI 투자대비 수익
A/B 테스트를
A/B Dashboard - 그로스 마케터
파이썬 - 데이터븐석가
신뢰수준 대신 유의수준을 지정. (파이썬이 먼저 지정)
유의수준 - 중심극한정리 복습
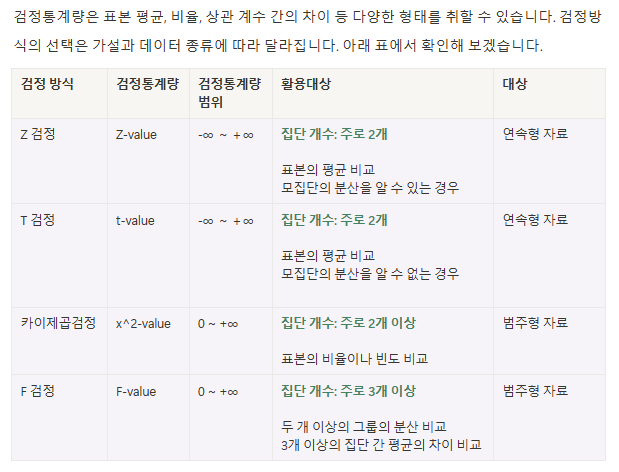
검정통계량
T 검정 - 모집단 크기/ 분산 알 수 알 수 있으면 Z검정/ 분산 알 수 없으면 T 검정
🚩 p-value: 어떠 사건이 우연히 발생할 확률 (Probability Value : 확률)

통계적으로 아무리 정답이어도, 데이터분석가는 의미가 있지만 데이터를 뜯어봐야함.
가설을 세우고 실제로 데이터가 어떻게 생겼는지 봐야함.
실습
# 라이브러리 호출
import pandas as pd
import numpy as np
# 과학 계산용 파이썬 라이브러리
import scipy.stats as stats
from PIL import Image
df = pd.read_csv("statistics.csv")
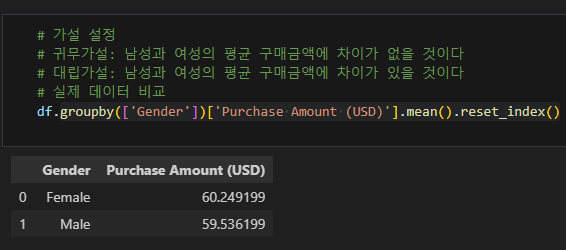
# 가설 설정
# 귀무가설: 남성과 여성의 평균 구매금액에 차이가 없을 것이다
# 대립가설: 남성과 여성의 평균 구매금액에 차이가 있을 것이다
# 실제 데이터 비교
df.groupby(['Gender'])['Purchase Amount (USD)'].mean().reset_index()
# 데이터 분리
# mask method
mask=(df['Gender']=='Male')
mask1 = (df['Gender']=='Female')
m_df = df[mask]
f_df = df[mask1]
[ ] 표로
[[ ]] 하면 데이터별로 슬라이싱
# 결제금액 컬럼만 가져오기
m_df=m_df[['Purchase Amount (USD)']]
f_df=f_df[['Purchase Amount (USD)']]
T-Test LL 가설검정 ( 너무 작은경우 )
# scipy 라이브러리를 이용해 t-score 와 pvalue 를 확인할 수 있습니다.
# t-test 는 표본의 평균(차이 분석)을 알고자 할 때 사용되며, 모집단의 분산을 알 수 없는 경우 주로 사용됩니다.
t, pvalue = stats.ttest_ind(f_df, m_df)
# t-score 는 그룹 간 얼마나 차이가 있는지에 대한 지표
# t-score 가 크면 그룹 간 차이가 큼을 의미합니다.
# p-value 는 우연에 의해 나타날 확률에 대한 지표입니다.
# p-value가 0.05 보다 크다 = 우연히 일어났을 가능성이 높다 = 연관성이 없다고 추정
# 여기서 p-value 값은 0.05 보다 크므로, 연관성이 없다고 추정할 수 있습니다.
# 대립가설 기각
# 귀무가설 채택
# 귀무가설: 남성과 여성의 평균 구매금액에 차이가 없을 것이다
(array ( [0.87691521]), array ([0.38058674]) )
t-valye -1~1 P-value 0.05 보다 큼. (우연임 - 대립가설 (성별과 구매금액 차이가 있다)이 연관이 없음 )
-> 실제 데이터 뜯어봤을 때도 연관이 없는지 한번 더 확인!
성별에 따른 구매금액이 관련이 없음 확인.
카이제곱 검정: 가설 설정하기 (범주형 데이터)
# 가설 설정
# 귀무가설: 성별과 구매Size 에는 관련성이 없을 것이다 (독립적일 것이다)
# 대립가설: 성별과 구매Size 에는 관련성이 있을 것이다
# 실제 데이터 비교
df.groupby(['Gender','Size'])['Customer ID'].count().reset_index()

카이제곱검정: 빈도표 그리기 pd. crosstab
#pandas 라이브러리의 crosstab 함수를 통해, 두 범주형 자료의 빈도표를 만들어 주겠습니다.
result = pd.crosstab(df['Gender'], df['Size'])
result

카이제곱검정: 가설검정
# 카이제곱 검정을 stat 함수를 통해 구현
# chi2_contingency를 통해, 카이제곱통계량, p-value를 출력할 수 있습니다.
stats.chi2_contingency(observed=result)
Chi2ContingencyResult(statistic=6.615107840598039, pvalue=0.08523181331915772, dof=3, expected_freq=array([[ 336.96, 561.6 , 212.16, 137.28], [ 716.04, 1193.4 , 450.84, 291.72]]))
# 각 값들을 별도로 보기
# 카이제곱 검정 통계량, pvalue, 자유도를 확인할 수 있습니다.
stats.chi2_contingency(observed=result)[0]
6.615107840598039
stats.chi2_contingency(observed=result)[1]
0.08523181331915772
# p-value 는 우연에 의해 나타날 확률에 대한 지표입니다.
# p-value가 0.05 보다 크다 = 우연히 일어났을 가능성이 높다 = 인과관계가 없다고 추정
# 여기서 p-value 값은 0.05 보다 크므로, 연관성이 없다고 추정할 수 있습니다.
# 대립가설 기각
# 귀무가설 채택
# 귀무가설: 성별과 구매Size 에는 관련성이 없을 것이다 (독립적일 것이다)
카이제곱검정 : 가설검정2
#자유도와 유의수준을 통해 귀무가설 기각 여부를 판단하기도 합니다.
#자유도란, 굉장히 복잡한 개념이므로,,, (변수1 그룹의 수-1)*(변수2 그룹의 수-1) 가 되겠습니다.
#(성별 2개 - 1 ) * (옷 사이즈 4개 -1 )
# 1*3 = 3 이 도출되었습니다.
stats.chi2_contingency(observed=result)[2]
# x 축은 유의수준, y 축은 자유도 입니다.
# 자유도3, 유의수준을 0.05 로 본다면, 7.81 검정통계량이 나오게 됩니다.
# 우리가 구한 카이제곱 검정통계량은 6.615 이므로 7.81 보다 작습니다.
# 표에 명시된 기준보다 값이 작을 경우 대립가설을 기각합니다.
# 대립가설 기각
# 이렇게까지는 잘 하지 않습니다..p-value 로 판단합니다.
Image.open('카이제곱분포표.png')

카이제곱 분포에서 연관이 없다라는게,,,
두 그릅간 분산의 차이에는 유의미한 발견이 되지 않는다.

4강 - 상관분석, 회귀분석
5강 - 실습
6강 - 분류분석, 군집분석, RFM 분석









